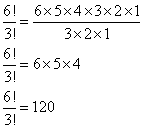ข้อที่ 21-25

21.ความสัมพันธ์ในข้อใดเป็นฟังก์ชัน

a.$\{(0,2),(0,3),(1,2),(3,4)\}$     $b.\{(0,0),(1,1),(2,3),(3,0)\}$       
c.$\{(1,1),(2,1),(2,2),(1,2)\}$     d.$\{(1,0),(0,3),(3,1),(1,4)\}$

แนวคิด

 

1.ตรวจสอบหาตัวเลือกที่ $x$ หนึ่งตัวจับคู่กับ $y$ เพียงตัวเดียว

$$A)\{(0,2),(0,3),(1,2),(3,4)\}$$

มี $(0,2)$ และ $(0,3)$ ที่ด้านหน้าเป็น $0$ เหมือนกัน แต่ด้านหลังเป็นคนละตัวกัน จึงไม่เป็นฟังก์ชัน

$$B)\{(0,0),(1,1),(2,3),(3,0)\}$$

ไม่มี x ตัวใดซ้ำกันเลย ความสัมพันธ์นี้จึงเป็นฟังก์ชัน

ตอบB

$$C)\{(1,1),(2,1),(2,2),(1,2)\}$$

มี $x=2$ ซ้ำ ไม่เป็นฟังก์ชัน

$$D)\{(1,0),(0,3),(3,1),(1,4)\}$$

มี $x=1$ ซ้ำ ไม่เป็นฟังก์ชัน



..........................................................................................................................................................

22.ถ้าช่วงเปิด $(a,b)$ เป็นเซตคำตอบของอสมการ

$$|x+1|+|4-2x|<9\text{ และ }x>3$$

แล้ว $a+b$ เท่ากับเท่าใด

a.3       b.5      c.7      d.9

 

แนวคิด
 

1.พิจารณาปลดค่าสัมบูรณ์กรณี $x>3$

เนื่องจาก $x>3$ ทำให้ $x+1$ มีค่าเป็นบวกเสมอ จึงทำให้ได้ว่า $|x+1|=x+1$ แต่ในขณะที่ $4-2x$ มีค่าเป็นลบเสมอ ดังนั้นเพื่อปลดค่าสัมบูรณ์แล้วต้องมีค่าเป็นบวก จึงทำให้ได้ $|4-2x|=-(4-2x)$ เมื่อปลดค่าสัมบูรณ์แล้วแทนค่าลงในอสมการจะได้

$$\begin{array}{rcl}|x+1|+|4-2x|& <& 9\end{array}$$
$$\begin{array}{r}\mathrm{}\\ (x+1)-(4-2x)& <& 9\end{array}$$

2.แก้อสมการ และหาค่า $a+b$

$$\begin{array}{rcl}x+1-4+2x& <& 9\end{array}$$
$$\begin{array}{r}\mathrm{}\\ \mathrm{ \; 3}x-3& <& 9\end{array}$$
$$\begin{array}{r}\mathrm{}\\ \mathrm{ 3}x& <& 9+3\end{array}$$
$$\begin{array}{r}\mathrm{}\\ \mathrm{ \; 3}x& <& 12\end{array}$$
$$\begin{array}{r}\mathrm{}\\ \mathrm{ \; x}& <\\ 4\end{array}$$

แต่เนื่องจากว่ามีเงื่อนไขว่า $x>3$

 

ดังนั้น คำตอบของอสมการจึงเหลือเพียง $3<x<4$ หรือเขียนเป็นเซตได้เป็น $(3,4)$
ดังนั้น $a=3$ และ $b=4$

ตอบ$\mathrm{ a}+b=7$

..........................................................................................................................................................

23.ลำดับเลขคณิต $-53,-46,-39,\cdots$ มีพจน์ที่มีค่าน้อยกว่า 200 อยู่กี่พจน์

 

a.25      b.32     c.37      d.43

      
 

แนวคิด

1.หาเทอมทั่วไป $a_n$ ของลำดับนี้

หาผลต่างร่วม $d$

$$\begin{array}{rcl}\mathrm{ \; d}& =& a_2-a_1\end{array}$$

$$\begin{array}{r}{\mathrm{}}_{}\\ & \; =& -46-(-53)\end{array}$$

$$\begin{array}{r}\\ & =& -46+53\end{array}$$

$$\begin{array}{r}\mathrm{}\\ & =& 7\end{array}$$

แทนค่า $a_1=-53$ และ $d=7$ ลงในสูตรรูปทั่วไปของลำดับเลขคณิต

$$\begin{array}{rcl}{a}_n& =& a_1+(n-1)d\end{array}$$

$$\begin{array}{r}\\ & \; =& (-53)+(n-1)\left(7\right)\end{array}$$

$$\begin{array}{r}\\ & \; =& -53+7n-7\\ & =& 7n-60\end{array}$$

ดังนั้น $a_n=7n-60$

2.แก้อสมการ $a_n<200$

$$\begin{array}{rcl}{\mathrm{ \; a}}_n& <& 200\end{array}$$

$$\begin{array}{r}\mathrm{}\\ 7\end{array}$$$$\begin{array}{rcl}n-60& <& 200\end{array}$$

$$\begin{array}{r}\mathrm{}\\ \mathrm{ 7}\end{array}$$$$\begin{array}{rcl}n& <& 260\end{array}$$

$$\begin{array}{r}\mathrm{}\\ \mathrm{ \; n}& <37.1\end{array}$$

ตอบมี 37 เทอมที่มีค่าน้อยกว่า 200

..........................................................................................................................................................
 

24.ถ้านำตัวอักษรทั้งหมดจากคำว่า DEGREE มาจัดเรียงเป็นคำต่างๆ โดยไม่จำเป็นต้องมีความหมาย จะจัดได้คำที่แตกต่างกันกี่คำ

a.120          b.134        c.144      d.64

แนวคิด

 

1.เรียงอักษรแบบมีบางตัวซ้ำ

อักษร D G R E E E มีตัว E ซ้ำ 3 ครั้ง จึงใช้วิธีเรียงอักษรทั้ง 6 ตัวโดยคิดว่าตัว E ทั้งสามต่างกันไปก่อน แล้วหารด้วย $3!$
จำนวนคำทั้งหมดเท่ากับ

ตอบ120 คำ

..........................................................................................................................................................

25.ต้องการจัดคน 7 คนนั่งบนรถโดยสาร 7 ที่นั่ง(รวมที่นั่งคนขับแล้ว) โดยมีคนขับรถเป็นเพียง 3 คน จะมีจำนวนวิธีการจัดได้กี่วิธี

  a.1440    b.1690     c.2160    d.720

 

แนวคิด

  

1.นับจำนวนวิธีเลือกคนขับ

มีคนขับรถเป็น 3 คน เลือกมาเป็นคนขับ 1 คน ได้

2.นับจำนวนวิธีจัดที่นั่งผู้โดยสารที่เหลือ

เมื่อเลือกคนขับไปแล้ว 1 คน คนที่เหลือมารวมกันเป็นผู้โดยสารทั้งหมด 6 คน  แล้วจัดที่นั่งให้กับคนทั้ง 6 ไปนั่งในที่นั่งที่แตกต่างกันทั้งหมด จึงเท่ากับการเรียงสับเปลี่ยนคน 6 คน

3.คำนวณจำนวนวิธีทั้งหมด

นำจำนวนวิธีใน 2 ขั้นตอนแรกมาคูณกัน

$$3\times 720=2160$$

ตอบ  2160