ถ้าสุ่มหยิบสมาชิก (xyzx)
a.
 b.
b. c.
c. d.
d.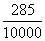
แนวคิด
ถ้า x=1
y>1และz>1
ทำนองเดียวกัน z∈S
เนื่องจากตำแหน่งของ y
(จำนวน y ที่เป็นไปได้)×(จำนวน z ที่เป็นไปได้)=9×9=92 เมทริกซ์
ในกรณีที่ x=2
y>2และz>2
ซึ่งมี y>2
และมี z>2
และจำนวนเมทริกซ์ที่มี x=2
(จำนวน y ที่เป็นไปได้)×(จำนวน z ที่เป็นไปได้)=8×8=82 เมทริกซ์
จากสองขั้นตอนที่แล้ว เราพบว่า
ถ้า x=19
เมทริกซ์
ถ้า x=28
เมทริกซ์
เมื่อเราทดลองเพิ่ม xถ้า x=2
x=3
ซึ่งจะมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 727
เมทริกซ์
x=4
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 626
เมทริกซ์
x=5
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 525
เมทริกซ์
x=6
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 424
เมทริกซ์
x=7
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 323
เมทริกซ์
x=8
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 222
เมทริกซ์
x=9
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 121
เมทริกซ์
x=10
ดังนั้นจำนวนเมทริกซ์ที่มี x,y,zซึ่งจะมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 72
x=4
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 62
x=5
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 52
x=6
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 42
x=7
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 32
x=8
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 22
x=9
ซึ่งมีเมทริกซ์ ที่สอดคล้องกับอสมการดังกล่าว ทั้งหมด 12
x=10
n(E)=92+82+72+⋯+32+22+12=12+22+32+⋯+92=9∑k=1k2
เมื่อใช้สูตรซัมเมชั่น
n∑k=1k2=n6(n+1)(2n+1)
จะได้
n(E)=9∑k=1k2=96(9+1)(2(9)+1)=96(10)(19)=285
ดังนั้นจำนวนเมทริกซ์ที่สอดคล้องกับอสมการทั้งสองเท่ากับ n(E)=285
4.นับจำนวนเมทริกซ์ทั้งหมดใน M
เมทริกซ์ใน M สร้างจาก x,y,z ซึ่งอยู่ในตำแหน่งที่แตกต่างกันในเมทริกซ์ (xyzx) ซึ่งตำแหน่งที่ต่างกันมีความสำคัญ ดังนั้นจำนวนเมทริกซ์ทั้งหมดย่อมเกิดจากผลคูณของจำนวนวิธีเลือกตัวเลขมาใช้เป็น x,y และ z ซึ่ง x,y,z∈{1,2,3,⋯,10} โดยแต่ละตัวมีให้เลือก 10 ตัวเลข ดังนั้น
n(S)=(จำนวนวิธีการเลือก x)×(จำนวนวิธีการเลือก y)×(จำนวนวิธีการเลือก z)=(10)×(10)×(10)=1000
5.คำนวณความน่าจะเป็นที่ x<y
และ x<z
จากขั้นตอนก่อนหน้าที่ได้ว่า n(E)=285 และ n(S)=1000 จะได้ว่า
P(E)=n(E)n(S)=2851000=0.2850
..........................................................................................................................................................
แนวคิด
1.วาดกล่องสี่เหลี่ยม
โจทย์กำหนดให้กล่องสีเหลี่ยมมีความสูง 6 ฟุต เราจึงสมมุติความกว้างและความยาวเป็น x และ y ฟุต ตามลำดับ ได้

2.หาความกว้างและความยาวของกล่อง
สร้างสมการจากที่โจทย์กำนดให้ว่า มีความจุ 126 ความจุหาได้จาก กว้าง x ยาวx สูง
และจาก เส้นรอบฐานของกล่องยาว 20 ฟุต ได้ว่า
จากสองสมการเราสามารถแก้ระบบสมการหาค่า x และ y ได้ แต่ในข้อนี้ พี่สังเกตง่าย ๆ ว่า สองจำนวนคูณกันได้ 21 บวกกันได้ 10 คือ 7 กับ 3 ดังนั้นความกว้าง คือ 3 ฟุต และความยาว คือ 7 ฟุต
3.คำนวณพื้นที่ผิวของกล่อง
จากกล่อง กว้าง 3 ฟุต ยาว 7 ฟุต สูง 6 ฟุต
กล่องประกอบด้วย 5 หน้าด้วยกัน คือ ฐาน 1 หน้า ด้านที่เป็นความกว้าง 2 หน้า และด้านที่เป็นความยาว 3 หน้า
ดังนั้นพื้นที่ผิดทั้งหมดคือ
..........................................................................................................................................................
8.บริษัท เที่ยวทั่วไทย จำกัด ต้องการจัดนำเที่ยวสำหรับกลุ่มนักท่องเที่ยวไม่เกิน 40 คน โดยมีค่าเช่ารถ 10,000 บาท และค่าใช้จ่ายอื่น ๆ 250 บาทต่อคน ถ้าบริษัทคิดค่าบริการคนละ 600 บาท แล้ว จะต้องมีนักท่องเที่ยวอย่างน้อยที่สุดกี่คนบริษัทจึงจะได้กำไรไม่น้อยกว่า 2,000 บาท
แนวคิด
1.สร้างสมการกำไร เพื่อหาจำนวนคนที่โจทย์ถาม
จาก
สมมุติให้มีคนใช้บริการทั้งหมด x คน
บริษัทคิดค่าบริการคนละ 600 บาท รายได้ที่ได้ คือ 600x บาท
ต้นทุนมี 2 ส่วน คือ ค่าเช่ารถ 10,000 บาท และค่าใช้จ่ายอื่น ๆ 250x บาท ดังนั้นต้นทุนทั้งหมด คือ 10,000
ได้ว่ากำไร คือ
โจทย์ต้องการกำไรมากกว่า 2,000 บาท
ดังนั้นจะต้องมีนักท่องเที่ยวน้อยที่สุด 35 คน ถึงจะได้กำไรมากกว่า 2,000 บาท
..........................................................................................................................................................
9.ข้อใดถูก
1.พิจารณาแต่ละตัวเลือก
ตัวเลือก A "ข้อมูลที่จะวัดค่ากลางได้ต้องเป็นข้อมูลเชิงปริมาณเท่านั้น" ข้อความนี้ไม่ถูกต้องเพราะว่าข้อมูลเชิงคุณภาพสามารถวัดฐานนิยมได้ ซึ่งฐานนิยมถือเป็นค่ากลางค่านึง
ตัวเลือก B "กรณีที่ข้อมูลมีจำนวนน้อยควรใช้ฐานนิยมเป็นค่ากลางเพราะสามารถนับความถี่ของข้อมูลได้สะดวก" การที่มีข้อมูลจำนวนน้อยไม่จำเป็นจะต้องใช้ฐานนิยมอย่างเดียว ไม่มีข้อจำกัดนี้ในการวัดค่ากลาง ตัวเลือกนี้จึงไม่ถูกต้อง
ตัวเลือก C "ค่าเฉลี่ยเลขคณิตเป็นค่ากลางที่ไม่เหมาะสมกับข้อมูลที่มีบางค่าต่ำกว่าข้อมูลอื่น ๆ มาก" ข้อนี้กล่าวถูกต้องเพราะว่าเป็นข้อจำกัดในการใช้ค่าเฉลี่ยเลขคณิต
ตัวเลือก D "เนื่องจากมัธยฐานคือค่าของข้อมูลที่อยู่กึ่งกลางของข้อมูลทั้งชุด ดังนั้นมัธยฐานจึงใช้เฉพาะกรณีที่ข้อมูลมีจำนวนข้อมูลเป็นจำนวนคี่เท่านั้น" ข้อความนี้ไม่ถูกต้องเนื่องจากไม่ว่าจำนวนข้อมูลเป็นจำนวนคู่ หรือ จำนวนข้อมูลเป็นจำนวนคี่ เราก็สามารถหามัธยฐานได้
ตัวเลือก C กล่าวถูกต้อง
..........................................................................................................................................................
10.ข้อมูลสองชุดดังนี้
ข้อใด ผิด
เฉลยละเอียด
1.พิจารณาตัวเลือก a
ตัวเลือก a บอกว่า ค่าเฉลี่ยเลคณิตของข้อมูลชุดที่ 1 มากกว่าค่าเฉลี่ยเลขคณิตของข้อมูลชุดที่ 2 อยู่ 0.5
เราก็เริ่มตัวหาค่าเฉลี่ยเลขคณิตของข้อมูลทั้งสองชุดแล้วค่อยนำมาเปรียบเทียบกัน
คำนวณค่าเฉลี่ยเลขคณิตของข้อมูลชุดที่

คำนวณค่าเฉลี่ยเลขคณิตของข้อมูลชุดที่

ซึ่งค่าเฉลี่ยเลขคณิตของข้อมูลทั้งสองชุดห่างกัน 1 ไม่ใช่ 0.5 ได้ว่าตัวเลือก a กล่าวผิด เราสามารถตอบได้เลย
แต่สำหรับคนที่ไม่ได้เริ่มจากข้อ a เดี๋ยวพี่จะแสดงให้ดูว่าตัวเลือกอื่น ๆ กล่าวถูกต้องทั้งหมด
2.พิจารณาตัวเลือก b
ตัวเลือก b กล่าวว่า ข้อมูลทั้งสองชุดมีมัธยฐานเท่ากัน จากข้อมูล
ข้อมูลทั้งสองชุดตำแหน่งมัธฐาน คือ
เราจึงหาค่ามัธยฐานได้จากการนำตำแหน่งที่ บวกกับ ตำแหน่งที่ แล้วหาร
มัธยฐานของข้อมูลชุดที่
มัธยฐานของข้อมูลชุดที่
ซึ่งมีค่าเท่ากัน ตัวเลือก B กล่าวถูกต้อง
3.พิจารณาตัวเลือก C
ตัวเลือก C บอกว่า ฐานนิยมของข้อมูลทั้งสองชุดนี้ต่างกันอยู่ 2
ฐานนิยมของข้อมูลชุดที่ 1 คือ 3
ฐานนิยมของข้อมูลชุดที่ 2 คือ 5
ซึ่งต่างกันอยู่ ตัวเลือก C กล่าวถูกต้อง


